PM Quadtree
Revision as of 01:28, 12 May 2012 by Dwh (talk | contribs) (→PM2 Quadtree: remove the trailing comment under bullet 2. the external reference no longer exists, and i can't see why this statement would be a problem.)
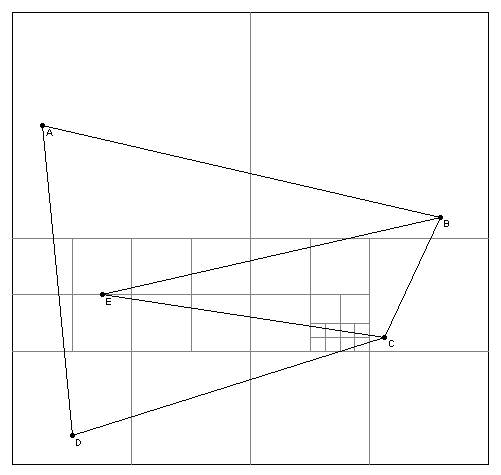
A PM (Polygonal Map) Quadtree describes a collection of quadtrees that can store points and edges. A q-edge refers to a subset of an edge formed by the partitions of the PM Quadtree.
PM1 Quadtree
A PM1 Quadtree follows the following rules:
- At most, one vertex can lie in a region represented by a quadtree leaf node.
- If a quadtree leaf node's region contains a vertex, then it can contain no q-edge that does not include that vertex.
- If a quadtree leaf node's region contains no vertices, then it can contain, at most, one q-edge.
- Each region's quadtree leaf node is maximal.
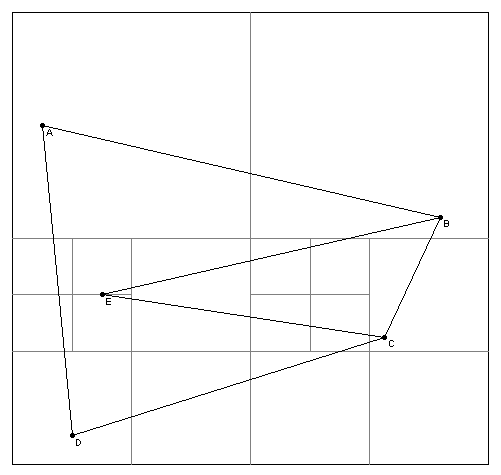
PM2 Quadtree
A PM2 Quadtree follows the following rules:
- At most, one vertex can lie in a region represented by a quadtree leaf node.
- If a quadtree leaf node's region contains a vertex, then it can contain no q-edge that does not include that vertex.
- If a quadtree leaf node's region contains no vertices, then it can contain only q-edges that meet at a common vertex exterior to the region.
- Each region's quadtree leaf node is maximal.
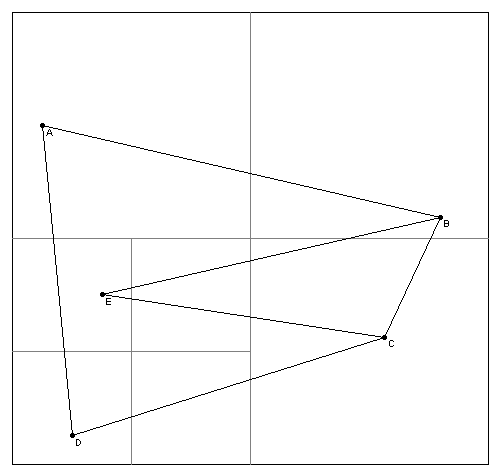
PM3 Quadtree
A PM3 Quadtree follows the following rules:
- At most, one vertex can lie in a region represented by a quadtree leaf node.
- Each region's quadtree leaf node is maximal.
Applications
PM Quadtrees are useful in determining the region in which a point lies, the determination of the boundaries of all regions lying within a given distance of a point, and overlaying two maps.